エタンデュとラグランジュ・ヘルムホルツの法則 照明光学系を開発、検討を行う際に不可避な代表的な法則がラグランジュ・ヘルムホルツの法則であり、代表的な定義がエタンデュであります。この関係性は物理法則として不変のものであり、これを逸脱する事はどんな光学設計者にも困難です。照明光学系としての要望を受けた際に、詳細な検討を実施する事なく実現困難と判断される最も多いケースは、この考え方に反している事例と言えるでしょう。 <エタンデュとは> 定義としては、「<光束断面積>と<光の立体角>との積」として定義されます。 エタンデュEは、下記数式にて規定されます。 E = π x A x (NA)^2 A:光束の断面積(光源の面積と捉えても結構です) π x (NA)^2 :放射立体角 立体角とは、半径=1の球体から錐面が形成する面積のサイズを示したものです。

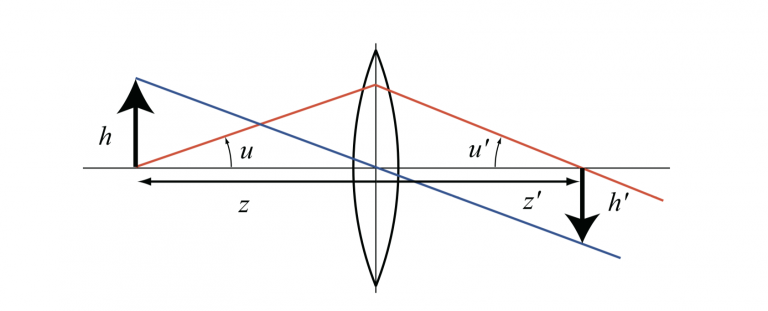
エタンデュは、すなわち光源そのものの明るさの質そのものを示しており、光学系がどれだけ有効に光を利用できるかを示す大きな指標となります。また、それだけではなくエタンデュはどのような複雑な光学系を介したとしても、常に保存量として不変です。光源発光面から照射面に至るまで、常にこの関係は保存されるため照明光学系において最も重要なファクターであります。 このエタンデュの保存法則と同様に扱われるのが、ラグランジュ・ヘルムホルツの法則です。 hu = h’u’

近軸光学における重要な関係である、「横倍率」と「角倍率」の逆数関係を支える法則ともいえるでしょう。横倍率β=h’/hであり、角倍率ν=u’/uですから、逆数関係が成立している場合にラグランジュ・ヘルムホルツの法則が成立することになります。光学系により像が拡大された場合には、光束の広がり角が狭くなるということを示しています。 この法則は、エタンデュの保存に直接結びつく「輝度不変則」理論の根底をなしているわけです。 異なる言葉で表現され、近軸光学と照明光学の区分けこそあれ根底の考え方が同一の両法則を真の意味で理解しているかどうかで効率的な照明光学系の基本検討が可能になる一助となります。